SMM C/P CME Event

21 October 1984 --- Day of Year (DOY): 295

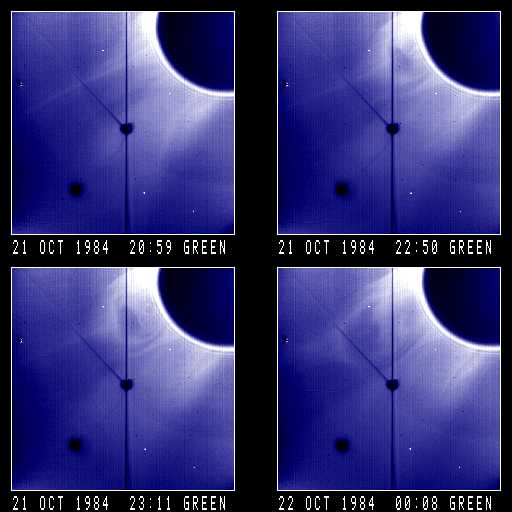
These four images, taken by the SMM Coronagraph, show a loop/cavity and core being ejected over the northeast limb of the sun. Solar north is to the upper left in each image, and the east equator points toward the lower left corner in each image.

Event Description

Loop/Cavity and core superposed on streamer. Defletions. Streamer is disrupted.

Event Properties

Start/Stop Times in SMM Coronagraph Field of View: October 21 ~21:37 to October 22 ~08:38
Central Position Angle: ~064 degrees
Width (in degrees): ~058
Speed (in km/sec): 205 <--- Outer Loop
Speed (in km/sec): 298 <--- Outer Cavity
Speed (in km/sec): 112 <--- Core

Image List:

October 21, 1984: 20:59 UT October 21, 1984: 22:50 UT

The SMM image at 22:50 is a partial image. The remaining bottom 1/3 of the data was lost during ground transmission.

October 21, 1984: 23:11 UT October 22, 1984: 00:08 UT

October 22, 1984: 00:46 UT October 22, 1984: 01:43 UT

October 21, 1984: 4 pictures in one frame

Detailed information on all SMM mass ejections is available in the SMM Catalogue of Coronal Mass Ejections